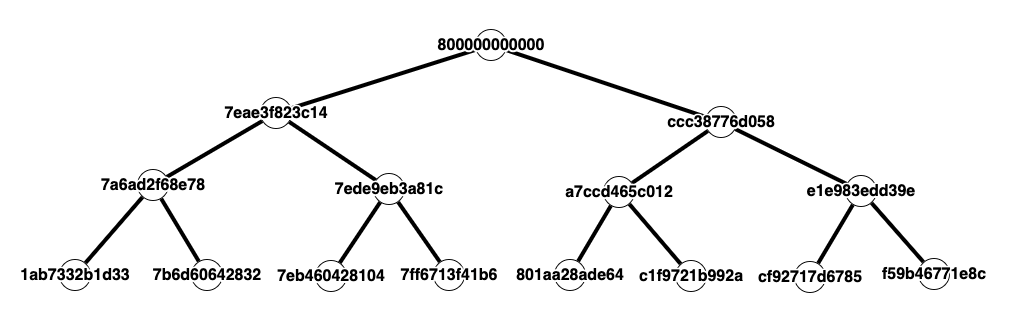
Index tree

Back onboard, preparing to continue your journey home to Earth, you install an update into the navigation computer.

The navigation computer stores many thousands of points of interest that ships may wish to travel to. To allow efficient searching through this dataset, it is indexed with a binary search tree.

Wanting to ensure the update has compiled the binary search tree correctly, you decide to manually replicate the index. You extract just the item ID numbers (your input data) and set about manually verifying the size and shape of the binary search tree.

Process the input data, placing each value into a binary search tree in the order it is given to you (ie: don't pre-sort the data). Calculate the maximum depth and the maximum width of the resulting binary search tree. Multiply the maximum depth by the maximum width to find your answer value.

Example 1

Using the following input data of hexadecimal integers...

80
64
c4
88
3a
d2
e3
6f
c6

The rules of a binary search tree require:

• If a number is less than the current node, go left
• If a number is greater (or equal) to the current node, go right
• When an empty location is reached, add a new node with the number in question.

Therefore the above data would construct a binary search tree that can be diagrammatically represented as follows...

             [80]
           /     \
        /           \
   [64]             [c4]
  /    \           /     \
[3a]  [6f]     [88]       [d2]
                          /   \
                      [c6]    [e3]

Considering this tree, observe it has a maximum depth of 4 (80-c4-d2-c6 or 80-c4-d2-e3) and a maximum width of 4 (3a-6f-88-d2). Accordingly in this example, the answer would be 16.

Your task

Process the input data of hexadecimal integers into a binary search tree. Multiply the maximum depth by the maximum width to find your answer value.

Hint

To help ensure you are processing the data correctly, the first 4 layers of the BST are shown here.